The equations for isotropic von Mises plasticity
The evolution of the stress is described by a system of differential equations,
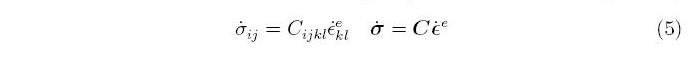
where the superscript e stands for elastic. An additive decomposition of the strain rate into elastic and plastic parts (indicated by a superscript p) is assumed,
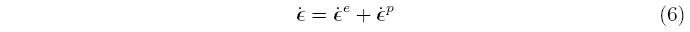
but it isn't unique; some formulations are based on a multiplicative decomposition of the deformation gradient into elastic and plastic parts. Using the additive decomposition, and solving for the elastic strain rate, the stress rate is expressed as
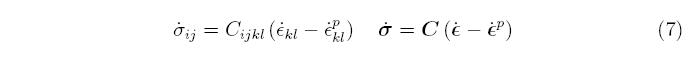
This equation contains both the unknown stress rate and the unknown plastic strain rate. A model for the plastic strain rate is described later. A basic goal of phenomenological plasticity models is to replicate the one-dimensional tension test. To achieve this, a scalar equivalent stress, σ is defined in terms of the stress tensor, an equivalent plastic strain, ε^-p is defined in terms of the plastic strain tensor, ε^p, and the equivalent stress is set equal to the yield stress,
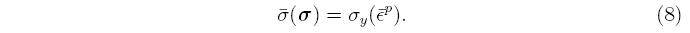
Because a six-dimensional stress space is being collapsed into a single number, there are many stress states that will produce the same equivalent stress, and they collectively define a surface in stress space. The particular collection of stresses that satisfy Equation 8 define a yield surface, and the normal to the yield surface is defined as
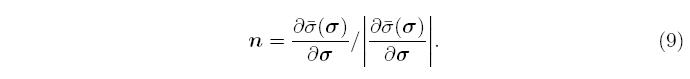
Plastic flow occurs when the stress is on the yield surface and the stress rate points outside the yield surface,
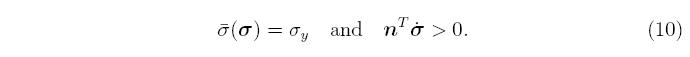
Inside the yield surface, σ^(σ) < σ y, the response is elastic regardless of the direction of the stress rate. When the response is elastic, the plastic strain rate is exactly zero, ε^p = 0. The choices for defining the equivalent stress and plastic strain aren't unique, but the choices made here are commonly used for modeling metals. The equivalent stress is the von Mises stress,
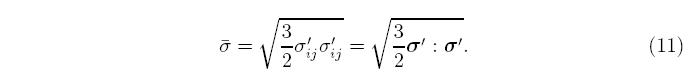
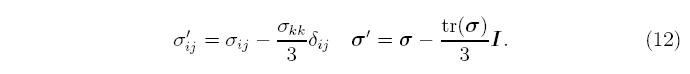
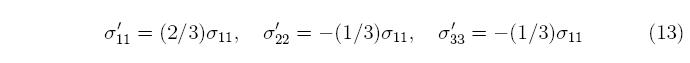
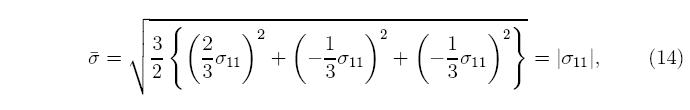
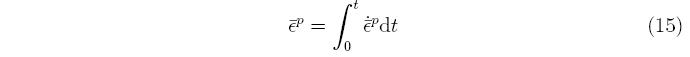
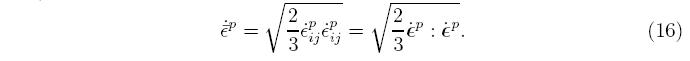
Note that there is no prime on the plastic strain rate; the plastic strain rate tensor is deviatoric in this model by construction. Plastic flow in metals is isochoric, meaning that the volume of the material is unchanged by plastic flow, which corresponds to a Poisson's ratio of 0.5. For uni-axial stress, the plastic strain rate has the form
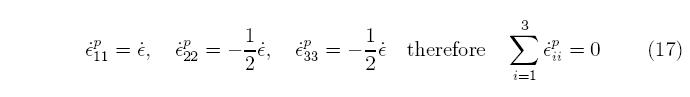
and all the shear strain rates are zero. The terms sum to zero, demonstrating that the plastic strain rate is deviatoric. Substituting in this plastic strain rate into Equation 16,
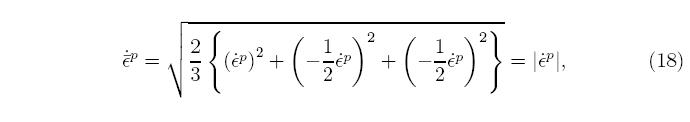
demonstrating that the multi-dimensional strain rate reduces to the onedimensional plastic strain rate. Drucker postulated associated flow, which says that the plastic strain rate is parallel to the normal to the yield surface,
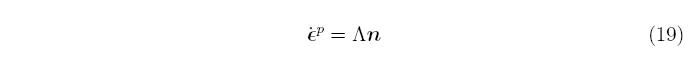
where is a proportionality constant that must be determined to complete the plasticity model. The proportionality constant is always greater than, or equal to zero, because a negative value implies that the response is elastic. The relation between ε^p and &lamda is obtained by substituting in the denition of the plastic strain rate into the denition of the equivalent plastic strain rate,
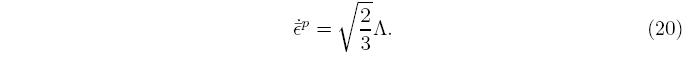
For the von Mises equivalent stress, the normal is
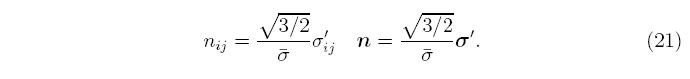
For linear, isotropic elasticity, expressed in terms of the Lame constants &mue and λ, the stress rate equation becomes
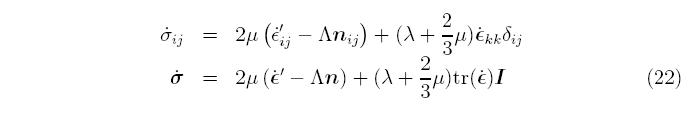
Substituting in the results of Equation 20 gives
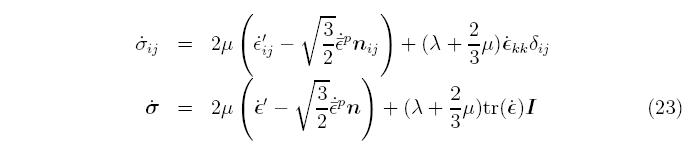
The rst term to the right of the equals sign defines the evolution of the deviatoric stress, while the second term governs the mean stress, which is the negative of the pressure, P. Note that the mean stress doesn't appear in the definition of the equivalent stress and its evolution isn't a function of the plastic strain rate. This allows the evolution of the deviatoric and mean stresses to be considered independently. A different definition of the equivalent stress (or equivalently, the yield surface) can lead to coupling between all the terms. To summarize the plasticity model, if the response is elastic, then
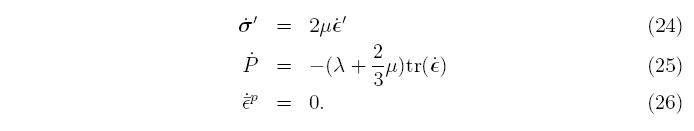
and if it is plastic, then
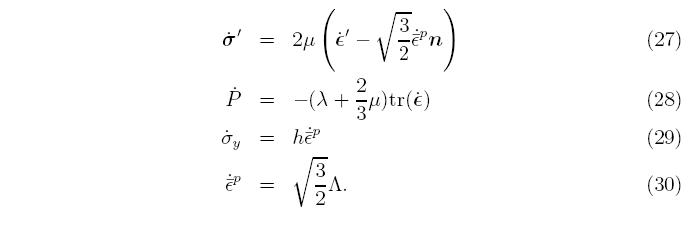
djb 2005
